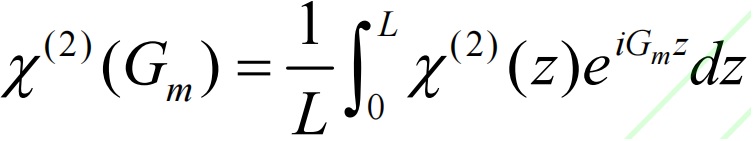Étude sur l'efficacité et la robustesse en température du cristal PPLN gazouillé dans une expérience de doublement de fréquence à 1064 nm - 03

2. Analyse théorique

2.2 Conception de la structure cristalline du CPPLN

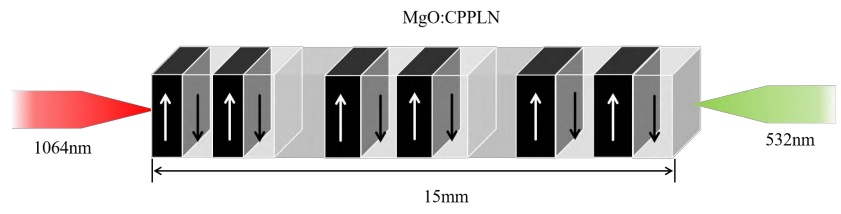
Afin d'obtenir une meilleure robustesse en température et une efficacité de doublement de fréquence plus élevée sur le même cristal CPPLN, nous avons conçu la structure cristalline du CPPLN. Le diagramme schématique du CPPLN pour le doublement de fréquence de 1 064 nm à 532 nm est présenté à la figure 1. Le faisceau incident avec une fréquence fondamentale est défini pour être de la lumière électronique, c'est-à-dire que sa direction de polarisation est horizontale. Dans le même temps, le faisceau de sortie est également réglé pour être un éclairage électronique. Ce paramètre nous permet d'utiliser la direction avec le plus grand coefficient non linéaire du second ordre dans le cristal CPPLN (d₃₃=27,2h/V).

Figure 1. Diagramme schématique du processus CPPLN SHG

Le but de cette expérience est d'améliorer l'efficacité de génération et la stabilité du faisceau laser de 532 nm. Par conséquent, la bande passante du gain doit être sélectionnée en fonction de la plage de température possible. Plus c'est petit, mieux c'est, pour garantir qu'une efficacité de doublement de fréquence plus élevée puisse être obtenue. La source de lumière de 1 064 nm utilisée dans cette expérience est un Nd:YVO auto-construit et pompé par LD.₄laser continu. Nous avons d’abord effectué un test de bande passante sur ce faisceau laser de 1 064 nm et avons constaté qu’elle était légèrement inférieure à 1 nm. Compte tenu de la nécessité de conserver une certaine marge, nous avons fixé la bande passante de gain du cristal à 1 nm. Selon la formule 4, la période initiale de CPPLN est sélectionnée à 6,99μm, le gazouillis est de 0,21 μm^-2, le nombre de périodes est de 2 104 et le rapport cyclique est de 49,61 %. Pour le cristal CPPLN, son coefficient de Fourier effectif peut être exprimé dans le domaine vectoriel de réseau réciproque comme(Formule 5) :

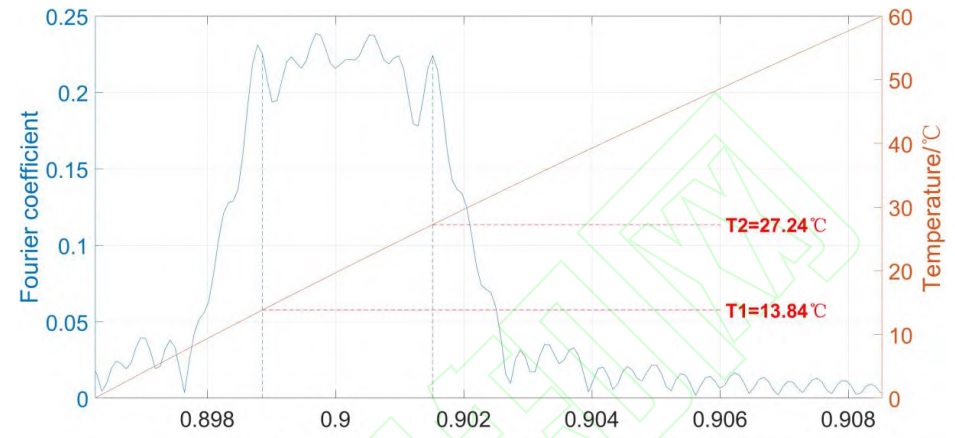
Afin de voir intuitivement les performances du CPPLN de cette structure de conception, nous utilisonsle F ci-dessusormula 5 pour effectuer une transformation de Fourier sur la distribution deχ⁽²⁾(z) de cette structure, et obtenir le coefficient de Fourier effectif de la structure CPPLN par rapport à la distribution vectorielle de réseau réciproque (comme le montre la figure 2), et mettre également la relation entre la température et le décalage de phase correspondant Δkdans la figure 2 pour une analyse comparative. DansFfigure2,T1 etT2 se trouvent aux deux extrémités de la partie convexe de la courbe d'indice de réfraction, correspondant aux vecteurs de réseau réciproques qui peuvent compenser le décalage de phase à des températures de 13,84 ℃ et 27,24 ℃.respectivement. La figure 2 montre que le vecteur de réseau réciproque fourni par le cristal CPPLN de cette structure peut compenser le décalage de phase dans la plage de 13,84 ℃ à 27,24 ℃, c'est-à-dire que dans cette plage de température, la lumière émise en fréquence doublée par le CPPLN sera toujours être maintenu à un niveau élevé.

Figure 2. Vecteur de réseau réciproque / Inadéquation de phase (µm^-1)

DepuisFSelon la formule 1, nous pouvons savoir que la raison principale des différentes efficacités de doublage de fréquence des cristaux doublants de fréquence fabriquésdepuisdifférents matériaux sont la différence d'indice de réfractionpourlelumière fondamentale etlefréquence doublant la lumière et la différence dans le coefficient non linéaire effectif du cristal lui-même. Selon l'équation de Sellmeier, nous pouvons calculer l'indice de réfraction de la lumière à 1064 nm et 532 nm dans le cristal CPPLN et le cristal LBO respectivement comme suit :n_{1, CPPLN}=2.1483,n_{2, CPPLN}=2.2246,n_{1, LBO}=1.6053,n_{2, LBO}=1.6054. D’après la figure 2, en utilisant la relationd_eff,CPPLN=χ⁽²⁾(g_m)*d₃₃, nous pouvons obtenir le coefficient non linéaire effectif du CPPLN conçu dans des conditions de quasi-adaptation de phase commed_eff,CPPLN=18h46/V. Le coefficient non linéaire effectif du LBO peut être calculé par le logiciel SNLO commed_eff,LBO=13h83/V. Les calculs montrent que dans des conditions idéales, l'efficacité de doublement de fréquence du CPPLN sera nettement supérieure à celle du LBO, atteignant 24,47 fois celle du LBO.