Étude sur l'efficacité et la robustesse en température du cristal PPLN gazouillé dans une expérience de doublement de fréquence à 1064 nm - 02

2. Analyse théorique

2.1 Robustesse en température

La robustesse à la température fait référence à la stabilité du cristal doublé en fréquence par rapport à la température. Plus précisément, lorsque la température fluctue, la puissance de la lumière dont la fréquence est doublée ne sera pas grandement affectée. L'influence de la température sur le processus de doublement de fréquence provient principalement de l'influence sur le décalage de phase. Pendant le processus de doublement de fréquence, dans le cas d'une faible approximation du signal, la puissance de la lumière doublée de fréquence peut être exprimée comme suit :

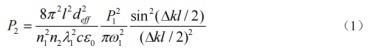
Danséquation 1,jeest la longueur du cristal doubleur de fréquence ;d_effest le coefficient non linéaire effectif ;cest la vitesse de la lumière dans le vide ;ε₀est la constante diélectrique du vide ;P._je,λ_je,n_je, etω_jesonttLa puissance, la longueur d'onde, l'indice de réfraction et le rayon de taille du faisceau duFfréquence fondamentalefaisceauet fréquence-douterdirigéfaisceaurespectivement. Til souscritje=1, 2 correspondent à la fréquence fondamentalefaisceauet la fréquence a doubléfaisceaurespectivement; la quantité de décalage de phase Δk=k₂-2k₁,dans quelle vague vsecteurk_je=(n_je2π)/λ_je. On peut le voir à partir de l'équation1 que seulement lorsque la condition d’adaptation de phase est remplie, c’est-à-dire lorsque Δk= 0, la puissance optique maximale doublée en fréquence peut être obtenue. Dans le processus d'adaptation quasi-phase, puisque la direction de polarisation spontanée du cristal non linéaire est artificiellement et périodiquement modifiée, la période de polarisationΛintroduira le vecteur de réseau inverseg_m. La relation entre le vecteur de réseau inverse et la période de polarisation est la suivante :

g_m=m(2π/Λ) (2)

Wicimreprésente lenombremordre quasi-adaptation de phase.Alorsle décalage de phase dans le processus de doublement de fréquence peut être réécrit comme:

Δk'=k₂-2k₁-g_m(3)

On sait par leSéquation d'Ellmeier :wLorsque la température change, l'indice de réfractionn_jesera également affecté, ce qui à son tour affecte le décalage de phase Δk. Depuis la période de polarisation du PPLN(www.wisoptic.com)est une période unique et le vecteur réciproque introduit est une valeur fixe, correspondance de phase Δk'= 0 ne peut être atteint que dans des longueurs d'onde spécifiques et des conditions de température spécifiques.Doncnous pouvons savoir que le point clé pour atteindre la robustesse en température est d'élargir la bande passante de gain du cristal polarisé afin que le vecteur de réseau inverse puisse couvrir une certaine plageetle décalage de phase peut toujours satisfaire Δk'= 0 lorsque la température change.jeEn d’autres termes, la robustesse en température est liée à la bande passante de gain du cristal. Plus la bande passante de gain est grande, meilleure est la robustesse du cristal en température. La période de polarisation du PPLN peut être exprimée en fonction de la positioncomme suit:

Dans la formule,D_gest le degré de chirp du cristal CPPLN(www.wisoptic.com), etΛ₀est la période initiale du CPPLN. On peut le voir depuisEéquation 4 que couvre la période de polarisation du CPPLNΛ₁= 2πΛ₀etΛ₂=Λ₀/[(1+D_gΛ₀je)/2π]. Et cela change continuellement dans cette plage, c'est-à-dire que le CPPLN de cette structure peut fournir un vecteur de réseau inverse qui change continuellement dans une certaine plage. Lorsque le décalage de phase k change dans cette plage en raison de la température, le vecteur de réseau inverse du CPPLN compensera parfaitement sa valeur changeante pour garantirΔk' = 0, c'est-à-dire que l'efficacité de conversion de la lumière à fréquence doublée peut être maintenue à un niveau très élevé dans une certaine plage de température. Cependant, il convient de noter que plus la plage de périodes de polarisation du CPPLN n'est pas meilleure, car l'augmentation du chirp entraînera une réduction du coefficient non linéaire effectif. Par conséquent, dans le processus de production lui-même, un équilibre doit être trouvé entre la robustesse à la température et l’efficacité de multiplication de fréquence la plus élevée.